CARTAN (É.)

CARTAN (É.)

Élie Cartan fut l’un des plus grands mathématiciens de son époque. Il possédait une intuition géométrique remarquable, aidée par une très grande aptitude à dominer les calculs les plus complexes. Il fut également un excellent professeur. Son œuvre considérable présente une grande unité; elle gravite principalement autour de la théorie des groupes de Lie, systèmes différentiels, «groupes infinis» et de leurs applications à la géométrie différentielle ainsi qu’à la mécanique. É. Cartan fut un précurseur et, dans beaucoup de domaines, il fut à l’origine du développement des mathématiques modernes.

Étude des groupes de Lie et applications géométriques

Élie Cartan, né à Dolomieu (Isère) et mort à Paris, fut élève de l’École normale supérieure, acheva sa thèse en 1894, puis enseigna aux universités de Montpellier, Lyon, Nancy et Paris. Après sa retraite en 1940, il eut encore une grande activité scientifique et continua à enseigner à l’École normale supérieure de Sèvres. Il était le père du mathématicien Henri Cartan.

Les premiers travaux de Cartan (et notamment sa thèse), à la suite de ceux de Lie et de Killing, de nature purement algébrique, sont consacrés à ce qu’on appelle maintenant les algèbres de Lie (ce qui revient à une étude locale des groupes de Lie). Cartan établit la classification des algèbres de Lie simples sur le corps des complexes (quatre classes plus cinq algèbres exceptionnelles). Il étudie les algèbres de Lie semi-simples et montre qu’elles sont caractérisées par une forme quadratique non dégénérée. Ensuite, il détermine les représentations linéaires irréductibles des algèbres de Lie semi-simples, ce qui lui permet notamment de découvrir les représentations spinorielles des algèbres de Lie orthogonales (on connaît l’importance de ces théories en physique). En 1914, Cartan établit la classification des algèbres de Lie simples sur le corps des réels.

Cartan applique la théorie des groupes de Lie à la géométrie différentielle; en 1910, il utilise les équations de structure de ces groupes pour établir une théorie du repère mobile qui étend les résultats de Frenet et Darboux à un espace homogène quelconque (c’est-à-dire un espace sur lequel opère transitivement un groupe de Lie G, ce qui est équivalent à E = G/H, H sous-groupe fermé de G); il étudie ainsi les invariants différentiels et le problème de la déformation des sous-variétés de E.

En 1922, Cartan (en relation avec la relativité), introduit la notion d’«espace généralisé» ou «non holonome» (comprenant notamment les espaces homogènes et riemanniens): il «attache» à chaque point d’une variété différentiable un espace homogène d’un groupe G et «raccorde» entre eux ces espaces; c’est la théorie des connexions (d’où les notions de courbure, torsion, groupe d’holonomie); en particulier la théorie des espaces à connexion euclidienne, affine, projective, conforme est développée. Depuis l’introduction des espaces fibrés qui a permis une formulation moderne de la notion de connexion (en particulier des «connexions de Cartan»), ces questions sont au cœur de la géométrie différentielle contemporaine.

Parmi les travaux les plus importants en géométrie de Cartan, figurent les espaces symétriques (en particulier les espaces riemanniens symétriques). Cartan a publié un livre et de nombreux mémoires sur la géométrie riemannienne.

C’est à partir de ces travaux que É. Cartan retourne à l’étude des groupes de Lie (cette fois du point de vue global); il déduit des propriétés topologiques globales des groupes simples, compacts ou non, à partir de celles des espaces symétriques. Il détermine notamment les nombres de Betti d’un espace symétrique à groupe d’automorphismes compact (il ramène ce problème à un problème algébrique).

Calcul différentiel extérieur

Ces derniers résultats utilisent la théorie des formes différentielles extérieures; cette théorie (aujourd’hui classique et d’une très grande utilité en mathématiques et en physique) est au centre de l’œuvre de Cartan. Partant de l’algèbre extérieure de Grassmann et généralisant les formes de Pfaff, Cartan a introduit (vers 1900) les formes différentielles extérieures et l’opérateur d de différenciation extérieure qu’il a utilisés pour établir les équations de structure des groupes de Lie, des «groupes infinis», pour formuler la théorie du repère mobile et des «espaces généralisés» (courbure, torsion d’une connexion). Les formes différentielles sont des éléments d’intégrales multiples et leur introduction a permis l’énoncé précis de la formule de Stokes. À partir de ces formes, Cartan a développé sa théorie des invariants intégraux (notamment dans son livre paru en 1922), généralisant les résultats de Poincaré, et donnant ainsi à la mécanique analytique une impulsion nouvelle. En s’appuyant sur les théorèmes de G. de Rham reliant l’homologie d’une variété à la cohomologie des formes différentielles (l’opérateur d vérifie d ² = 0), Cartan utilise les formes différentielles invariantes sous l’action d’un groupe, pour étudier les propriétés globales des espaces homogènes et groupes de Lie (voir ci-dessus).

Cartan a étudié les systèmes différentiels: d’abord les systèmes de Pfaff (vers 1900), puis, à la suite des travaux de Kähler, les systèmes extérieurs de degré quelconque (dans son livre sur les systèmes différentiels paru en 1945). Il développe sa théorie de l’involution (un système est involutif s’il existe une chaîne E¹ 說 ... 說 Eⁿ d’éléments de contact intégraux de ); pour les systèmes analytiques, on a le théorème d’existence de Cartan-Kähler (de caractère local), associant à une chaîne d’éléments de contact intégraux une chaîne de variétés intégrales. Cette théorie est liée également à la théorie du problème d’équivalence locale (c’est-à-dire de l’isomorphisme local de structures d’«espace généralisé»). De grands progrès ont été accomplis dans ces domaines (la théorie de l’involution, étudiée du point de vue algébrique, a été rattachée à des théories cohomologiques).

«Groupes continus infinis»

Les théories de l’équivalence et de l’involution ont leurs applications dans la théorie des «groupes continus infinis» développée par Cartan de 1904 à 1909 (résumée dans des exposés du séminaire Julia en 1937); un «groupe infini continu» (dont la définition a été donnée par S. Lie) est un ensemble d’homéomorphismes analytiques d’ouverts de Cⁿ (ou Rⁿ ), muni d’une loi de composition partiellement définie, constituant la solution générale d’un système S d’équations aux dérivées partielles analytiques, assujetti à certaines conditions de régularité (dont l’ordre est appelé l’ordre du «groupe infini»); si S est un système de Mayer-Lie (c’est-à-dire si toutes les dérivées partielles d’ordre 閭 r s’expriment en fonction des dérivées d’ordre inférieur), on a un «groupe continu fini»; comme n’est pas en général muni d’une structure algébrique de groupe, les notions d’isomorphisme, «sous-groupe» invariant, «groupe infini» simple, ne peuvent se formuler de la même manière que pour les groupes de transformations véritables; c’est pourquoi Cartan a introduit la notion de prolongement: face=F0021 opérant localement dans C^n+p (resp. R^n+p ) est le prolongement de opérant localement dans Cⁿ (resp. Rⁿ ), si tout f 捻 se projette suivant une application de f 捻 ; le prolongement est holoédrique, si à tout f 捻 correspond un seul homéomorphisme f 捻 ; il est mériédrique dans le cas contraire. Cartan a obtenu les trois théorèmes fondamentaux suivants, généralisant ceux de Lie pour les groupes de transformations:

1. Tout «groupe continu» admet un prolongement holoédrique du premier ordre (prolongement normal) caractérisé par la propriété de laisser invariantes des formes de Pfaff.

2. Ces formes 諸ⁱ vérifient des équations de structure:

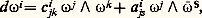les formes 諸^S étant définies sur un prolongement de l’espace où opère , les coefficients a ^ijs (nuls dans le cas fini) formant un système involutif.

3. À la donnée des coefficients c ^{i jk} et a ^{i js} vérifiant certaines conditions de compatibilité, il correspond un «groupe infini».

Cartan a déterminé les «groupes continus» isomorphes holéodriques d’un «groupe» donné et défini un «groupe continu» simple comme un «groupe» n’admettant pas de «groupe» isomorphe mériédrique. Par la considération des groupes linéaires irréductibles semi-involutifs, Cartan a obtenu la classification des «groupes infinis» simples transitifs: ceux-ci se répartissent en quatre classes.

Depuis 1952, avec l’introduction des pseudogroupes de Lie, ces questions ont pris un développement considérable: l’utilisation des jets et des feuilletages permet de formuler la théorie de Cartan sous forme globale (un «groupe infini» est un noyau de pseudogroupe de Lie). Beaucoup de travaux utilisent les pseudogroupes infinitésimaux (faisceaux d’algèbres de Lie), ce qui se rattache aux travaux de S. Lie et Vessiot, mais Cartan n’avait pas étudié ce point de vue.

Encyclopédie Universelle. 2012.